Вычисление процентов по формулам, примеры решения задач
Вычисление процента от определенного числа — одна из базовых математических операций. Вам точно придется столкнуться с ней в жизни. Формула процентов пригодится не только в школьных задачах по математике и физике. В различных бытовых ситуациях (от взятия ипотеки в банке до подбора пропорций ингредиентов для пудинга) приходится вычислять это значение.
Даже в ролевых играх характеристики вашего персонажа иногда модифицируются формулами с процентами. Ловко ориентируясь в этих математических действиях, вы будете иметь более четкое представление о многих окружающих вас явлениях.
Что такое один процент
Это одна сотая часть любого числа. Записанный дробью один процент равен 1/100, или 0,01. Показатель не выражает собственного значения. Он должен относиться к какому-либо числу. Процент показывает долю части от целого.
Принято считать, что любое исходное число - это 100 %. Если от него берется какая-либо часть, ее можно выразить в дробях или в процентах.
Очень важно понимать отношения между этими величинами, потому что они часто взаимозаменяемы. Например, в прессе можно встретить выражения "одна четвертая часть населения России" или "25 % населения России". Это одно и то же. В таблице приведены процентные меры, наиболее часто используемые людьми, а также соответствующие им дроби.
| Обыкновенная дробь | 1/2 | 1/3 | 2/3 | 1/4 | 3/4 | 1/5 | 1/10 |
| Десятичная дробь | 0,5 | ~0,33 | ~0,66 | 0,25 | 0,75 | 0,2 | 0,1 |
| Процент | 50 % | ~33,33 % | ~66,66 % | 25 % | 75 % | 20 % | 10 % |
Как видим, проценты весьма близки к десятичным дробям. Заменять один показатель другим очень просто. Чтобы перевести десятичную дробь в процент, нужно умножить ее на 100, то есть сместить запятую на два знака вправо. Вот несколько примеров:
- 0,23 × 100 = 23 %.
- 0,056 × 100 = 5,6 %.
- 0,9 × 100 = 90 %.
Если разделить число процентов на 100, сместив запятую на два знака влево, мы получим соответствующую ему десятичную дробь. Вот один пример:
- 23 %/100 = 0,23.
Рассмотрим несколько способов, как находить проценты. Формулы, представленные ниже, пригодятся и в школьных задачах, и в жизни.
Вычисление через нахождение одного процента
В большинстве задач довольно просто найти 1 % от данного числа. Зная эту величину, легко определить искомое число. Попробуем данный метод с разными типами задач.
Пример 1. Магазин обещает скидку 30 % при покупке на сумму от 5000 руб. Сколько денег мы сэкономим, если в чеке будет стоять цифра 5468 рублей?
Нам нужна формула вычисления процента от суммы. Пользоваться ею очень просто. Чтобы найти одну сотую долю, мы делим сумму покупки на 100, а полученный процент умножаем на 30:
- 5468 ÷ 100 = 54,68.
- 54,68 × 30 = 1640,4.
Подобные задания можно решать и в одно действие, если просто умножить данное число на нужный процент, переведенный в десятичную дробь:
- 5468 × 0,3 = 1640,4.
Поскольку дробь 0,3 соответствует 30 %, результат остается таким же. Мы сэкономим 1640,4 руб.
Пример 2. На мероприятие не пришли 12 % приглашенных. Известно, что это 15 человек. Сколько всего людей было приглашено?
Здесь необходимо вычислить общее количество по известной доле. Для этого мы разделим число на процент, а затем умножим найденное значение на 100:
- 15 ÷ 12 = 1,25.
- 1,25 × 100 = 125.
Как можно видеть, действия с числом 100 настолько просты, что их можно опускать. Задача решается в одно действие, если разделить известную долю людей на десятичную дробь, соответствующую проценту:
- 15 ÷ 0,12 = 125.
Было приглашено 125 человек.
Метод пропорций
Это очень удобный способ решать различные задачи на проценты. Пропорция в данном случае — это уравнение в виде двух дробей по разные стороны от знака "равно".
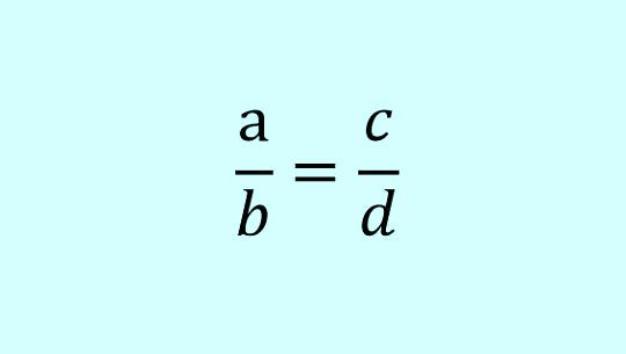
Прелесть пропорций в "правиле креста". Оно заключается в том, что произведения членов уравнения, лежащих крест-накрест, равны. Можно вывести из указанной выше пропорции следующее выражение:
- ad = bc.
Понимание этой математической зависимости значительно упрощает нахождение искомой величины. Чтобы найти любой из членов пропорции, нужно перемножить крест-накрест два известных числа и разделить на оставшееся. Чтобы было понятнее, стоит пояснить на примерах, которые уже приводились выше.
Для задачи под номером 1 пропорция будет выглядеть так, как на фото ниже.
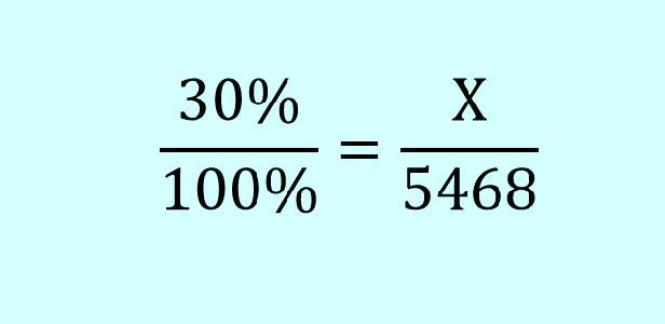
Чтобы найти количество сэкономленных средств, мы трансформируем уравнение следующим образом:
- Х = 30% × 5468 ÷ 100% = 1640,4.
Как видите, числа и действия те же, но метод пропорций добавляет задаче наглядности.
Для задачи под номером 2 пропорция приведена на следующем фото.
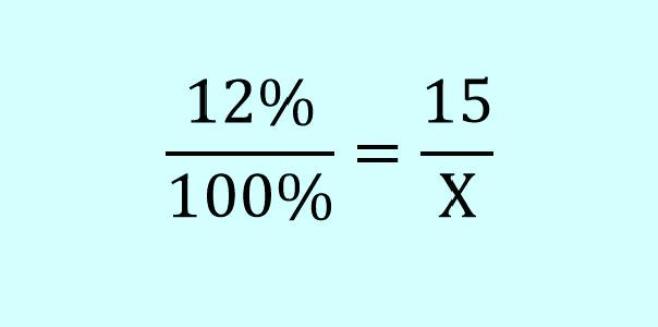
Соответственно, уравнение получится следующее:
- Х = 100% × 15 ÷ 12% = 125.
Вычисление процентных соотношений между числами
Иногда требуется найти, какую долю одно число составляет от другого. Мы можем вычислить эти проценты по приведенной на фото формуле.
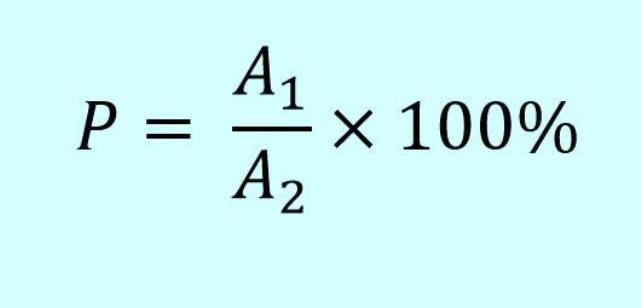
Р здесь — проценты, А1 — число, входящее в А2. Пользуясь формулой, можно найти, какой процент от зарплаты вы отдаете за квартиру. Так, если вы получаете 95 000 рублей в месяц и тратите на коммунальные услуги 19 000, порядок вычисления указан на картинке ниже.
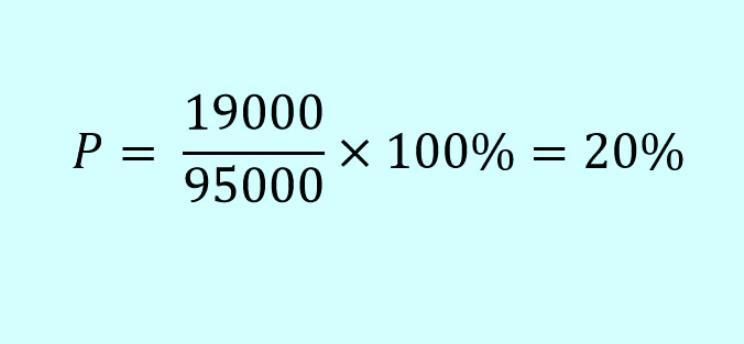
В этой формуле процентов можно увидеть видоизмененную пропорцию, что лишний раз показывает, насколько она универсальна.
Вычисление процентных соотношений не очень сложно. Эти действия используются не только математиками. Вычислить проценты по формулам должен уметь каждый взрослый человек, так как очень часто приходится сталкиваться с этим в различных жизненных ситуациях.
